Application to Curvilinear Geometries
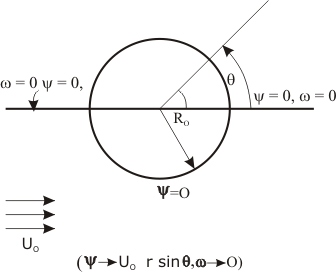
Figure 26.1: Flow Over a Circular Cylinder
Consider the steady, incompressible flow an infinitely long cylinder of radius 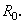
The stream function and vorticity equation for this flow geometry are given in terms of the cylinder polar coordinate 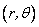 as: as:
where the redial and tangential velocity components are
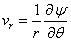 and 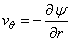 |
(26.3) |
The boundary conditions for stream function and vorticity have to be derived. The stream function must be a constant on the axis ( 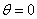 and and 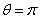 ) since ) since 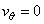 by the virtue of axisymmetry. On the solid surface, at by the virtue of axisymmetry. On the solid surface, at 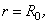 a constant stream line is obtainable, since the normal velocity a constant stream line is obtainable, since the normal velocity 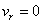 on the cylinder. For this flow configuration, the axis as well as the cylinder surface are the parts of the same streamline. The value of the stream function can be set equal to zero on these surfaces (Figure 26.1). Therefore, on the cylinder. For this flow configuration, the axis as well as the cylinder surface are the parts of the same streamline. The value of the stream function can be set equal to zero on these surfaces (Figure 26.1). Therefore,
We can write
|