Outflow Boundary
B4 is the outflow boundary (Fig. 25.1). If the outflow boundary conditions are know beforehand, then why are we computing? They are not known explicitly, but we can prescribe or set some gradients at the out let which are physically meaningful. We can imagine about continuative outflow conditions which will ensure smooth transition through the outlet boundary. For axial and normal velocities, we can impose less restrictive type condition, which are
Thoman and Szewczyk (1966) developed outflow boundary conditions through setting
Then, from 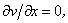 they derived they derived 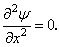 For constant For constant 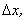 at at 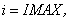 this gives: this gives:
However, some difficulties were experienced if the coefficients of 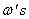 on the right hand side of equation (24.10) have a sum greater than unity. In that case, the process will diverge.The quantities, such as on the right hand side of equation (24.10) have a sum greater than unity. In that case, the process will diverge.The quantities, such as 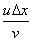 and and 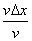 play a vital role in such cases. As a matter of fact, these quantities are mesh Reynolds number. By taking very small grid size, they may be kept below a desired small value of 2. Another remedy which could be applied along with, is to introduce a upwind bias. So the difference quotients with respect to convective components become play a vital role in such cases. As a matter of fact, these quantities are mesh Reynolds number. By taking very small grid size, they may be kept below a desired small value of 2. Another remedy which could be applied along with, is to introduce a upwind bias. So the difference quotients with respect to convective components become
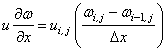 for 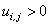 |
(25.14) |
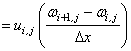 for for 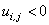
|
(25.15) |
In a similar way, 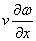 can be evaluated. These are then used in equation (24.9) for the subsequent development of equation (24.10) can be evaluated. These are then used in equation (24.9) for the subsequent development of equation (24.10)
Regarding the vorticity boundary condition given by equation (25.2) it can be said that the condition is first order accurate. The accuracy can be increased and we can try for a second order accurate boundary condition.
|