Boundary Condition
Now let us discuss about the boundary conditions.
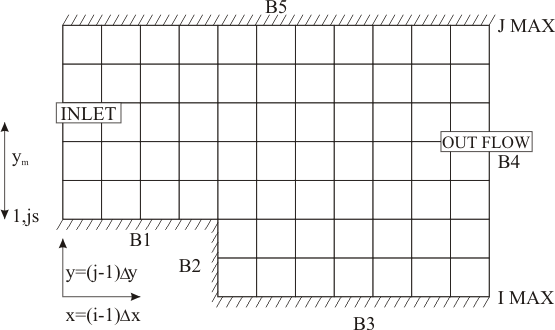
Figure 25.1
Consider Fig. 25.1, we shall call B1 and B3 as bottom wall. Similar kind of boundary conditions are aplicable on B1 and B3. At the nodal points which are coinciding with the solid wall we can directly put 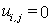 and and 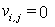 Since the line B1-B2-B3 is a streamline, any constant value of Since the line B1-B2-B3 is a streamline, any constant value of 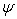 on it is acceptable. The usual choice is on it is acceptable. The usual choice is 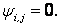 The wall vorticity is an extremely important evaluation. At no-slip boundaries, The wall vorticity is an extremely important evaluation. At no-slip boundaries, 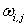 is produced. It is the diffusion and subsequent advection of the wall produced vorticity which governs the physics. Using boundary B1 as an example, we expend is produced. It is the diffusion and subsequent advection of the wall produced vorticity which governs the physics. Using boundary B1 as an example, we expend 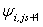 by a Taylor series as by a Taylor series as
But 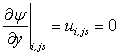 by no-slip condition and by no-slip condition and 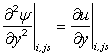 |
Again, 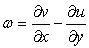 |
Along the wall, 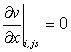 [because [because  constant constant 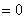 ]. ]. |
Thus, 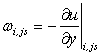 |
Substituting this into (25.1) and solving for 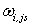 with with 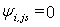 gives gives
More general from regardless of the wall orientation or value of 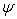 at the boundary, it can be written as at the boundary, it can be written as
where 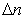 is the distance from is the distance from 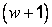 to ( to (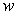 ) in the normal direction [ ) in the normal direction [ 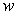 denotes at the wall]. denotes at the wall].
|