The Galerkin's weighted residual minimization approach of Eq. (18.5) yields
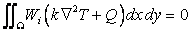 for 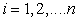 |
(19.1) |
where 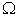 is the solution domain and is the solution domain and 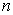 is the number of unknown temperatures. is the number of unknown temperatures.
In the Galerkin's method, the weighting function 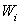 are the same as the interpolation (basis) function are the same as the interpolation (basis) function 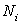 which are used for defining the variation T between the nodal points. Let which are used for defining the variation T between the nodal points. Let 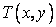 be the trial solution. Thus the residual equation can be written as be the trial solution. Thus the residual equation can be written as
In the above form, the requirement on 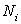 is that it must be atleast twice differentiable so that a non-trivial is that it must be atleast twice differentiable so that a non-trivial 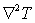 value can be obtained at all locations. However, this requirement can be weakened by integrating the value can be obtained at all locations. However, this requirement can be weakened by integrating the 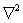 operator by parts. operator by parts.
In addition to the convenience of using lower order interpolation functions, the weak formulation also introduces the boundary conditions of the problem in a suitable fashion. The intergration by parts can be carried out using the divergence theorem as follows:
where 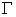 is the boundary of the domain is the boundary of the domain 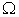 . Thus the residue equations take a final form (after a sign change) . Thus the residue equations take a final form (after a sign change)
Substitutions for the boundary integral term in terms of the given boundary conditions
where the terms have been numbered as 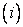 to to 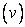 for our future reference. for our future reference.
|