Introduction
In finite element technique, the nodal equations for the field variables are obtained through an integral formulation, which may be set up through a variational principle (if one exists), or through the Galerkin's weighted residual approach. Here we shall consider the Galerkin's approach, which has a general applicability. Let us consider a general representation of a differential equation on a region 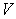
For the one dimensional heat conduction equation, the governing differential equation is
The symbol 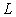 is an operator is an operator
that is operating on 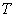 . The exact solution requires to satisfy Eqn. 18.1 at every . The exact solution requires to satisfy Eqn. 18.1 at every 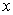 points. Let us seek for an approximate solution points. Let us seek for an approximate solution 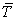 that introduces an error that introduces an error 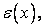 called the residual called the residual
The approximate methods are centered around the concept of setting the residual relative to a weighting function 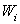 to zero to zero
The 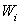 can be chosen based on the guiding philosophies of different variants of the weighted residual methods. In the Galerkin method, the can be chosen based on the guiding philosophies of different variants of the weighted residual methods. In the Galerkin method, the 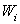 are chosen from the basis functions used for constructing are chosen from the basis functions used for constructing 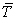 . We shall deal with this aspect, in detail, in the subsequent sections. . We shall deal with this aspect, in detail, in the subsequent sections.
|