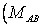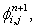In Eqn. (17.4) the geometrical quantities and , etc. ) need to be evaluated only once for a given grid and used for all subsequent calculations, Equation (17.4) is solved conveniently using a Successive Over-Relaxation (SOR) technique. Equation (17.4) is manipulated to give an estimate of thus

and the improved better value is

where 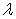is the relaxation parameter.

One attractive feature of the finite volume method is that Neumann (derivative) boundary conditions can be handled as readily as Dirichlet boundary conditions by direct substitution into Eqn. (16.3).

The discretised Equation (17.4) reduce to the centred finite difference scheme on a uniform rectangular grid