When the boundary temperature is specified, the control volume shapes near the boundary can be changed to facilitate the implementation of the boundary conditions.
For instance, consider the condition T = TL on the x = L boundary (see Fig. 14.4).
For the nodes on the boundary, an imaginary extension of the control volumes outside the actual domain can be considered in line with the finite difference methodology described earlier. The physical boundary is taken to be at the center of “boundary cell” of width 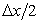 (see Figure 14.4), while the widths of the adjacent cells are thus reduced to 
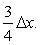
Consider a typical control volume i near the x = L boundary as shown in Fig. 14.4
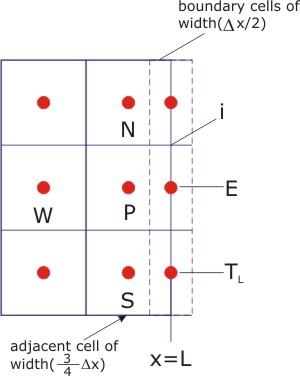
Figure 14.4: Boundary Condition, at x = L , T = TL.
The boundary cells will need no nodal equation as the T = TL will be applied. The nodal equation for the adjacent cell P will be written considering a shortened control volume:
where 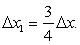 Note that TL has been used instead of TE in the above equation. So, the boundary condition is being directly applied.
In this fashion, by adjusting the control volume spacing and the placement of nodes, nodal equations can be obtained at all nodes and these can be solved simultaneously by the matrix inversion technique, line-byline technique or point-by-point technique as discussed earlier. Having done the above exercise, we may like to look at a more generalized description of the finite volume method.
Congratulations, you have finished Lecture 14. To view the next lecture select it from the left hand side menu of the page or click the next button. |
