The Basic Technique
We have introduced the finite difference method. In the context of the method of weighted residuals, it can be said that the Finite Difference procedure is a collection method with piecewise definition of the field variable in the neighborhood of chosen grid points (or collection points).
In a similar fashion the Finite Volume Method is a subdomain method with piecewise definition of the field variable in the neighborhood of chosen control volumes. The total solution domain is divided into many small control volumes which are usually rectangular (or arbitrary quadrilateral in shape. Nodal points are used within these control volumes for interpolating the field variable and usually, a single node at the centre of the control volume is used for each control volume. This method was developed by Patankar and Spalding (1972) and they proposed the use of the physical approach (where possible) for deriving the nodal equations. We shall illustrate the technique with the help of the 2-D heat conduction problem in rectangular geometry.
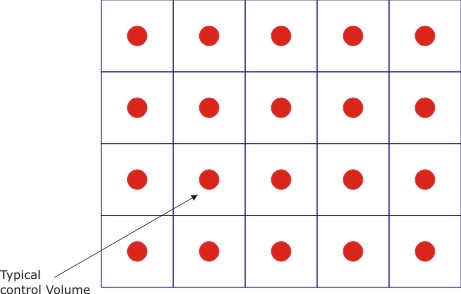
Figure 14.1: Grid Arrangement for the Finite Volume Method
Consider 2-D, steady heat conduction in rectangular geometry (Figure 14.1). The 2-D heat conduction equation is
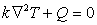 |
(14.1) |
where 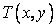 is the temperature field, is the temperature field, 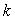 is the thermal conductivity and Q is the heat generation per unit volume. is the thermal conductivity and Q is the heat generation per unit volume.
At present we shall not consider any specific set of boundary conditions for the problem, but we shall discuss the handling of various type of boundary condition in due course. |