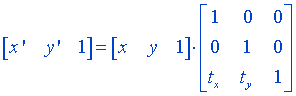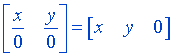ADVANTAGES OF HOMOGENEOUS COORDINATES

Representing all transformations as matrix multiplications

Two Dimensional coordinates  are represented using three-element column vectors, and Transformation operation is represented by 3 x 3 matrices.

which can be written in abbreviated form as

Capturing composite transformations conveniently

On the basis of the matrix product of the individual transformations we can set up a matrix for any sequence of transformation known as composite transformation matrix. For row-matrix representation we form composite transformations by multiplying matrices in order from left to right whereas in column-matrix representation we form composite transformations by multiplying matrices in order from right to left.

Non linear transformations (3D-perspective transformations)

For details Click Here

Representing points at infinity.

Homogeneous coordinates can be used to display a point at infinity. For example

In the above example the point at infinity is presented in the form of homogeneous coordinates. This is often needed when we want to represent a point at infinity in a certain direction. For instance, for finding the vanishing point in perspective projections we can transform the point at infinity in the given direction.