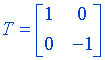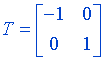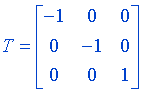REFLECTION

Reflection is nothing more than a rotation of the object by 180^o. In case of reflection the image formed is on the opposite side of the reflective medium with the same size. Therefore we use the identity matrix with positive and negative signs according to the situation respectively.

The reflection about the x-axis can be shown as:

The reflection about the y-axis can be shown as:

REFLECTION ABOUT A ORIGIN

When both the x and y coordinates are flipped then the reflection produced is relative to an axis that is perpendicular to x-y plane and that passes through the coordinate origin. This transformation is referred as a reflection relative to coordinate origin and can be represented using the matrix below.

REFLECTION ABOUT AN ARBITRARY LINE

Reflection about any line y= mx + c can be accomplished with a combination of translate-rotate-reflect transformations.

Steps are as follows

1. Translate the working coordinate system (WCS) so that the line passes through the origin.

2. Rotate the WCS such that one of the coordinate axis lies onto the line.

3. Reflect about the aligned axis

4. Restore the WCS back by using the inverse rotation and translation transformation.

REFLECTION ABOUT AN ARBITRARY POINT

As seen in the example above, to reflect any point about an arbitrary point P (x,y) can be accomplished by translate-reflect transformation i.e. the origin is first translated to the the arbitrary point and then the reflection is taken about the origin. And finally the origin is translated back to its original position.

The whole process can be visualized using the animation below.