Four Factor Formula

• In two group approach we shall have two groups of neutrons.
• One will be called fast and the other thermal.
• We had discussed in our previous lectures that the thermal group will have energy upto 5kT, while the fast group will have energies above 5kT.
• Such a division will eliminate up-scattering in thermal group.
• Let us now trace the history of a neutron which is thermal.

• Thus the cycle has been completed. By the definition of the infinite multiplication constant, we can write

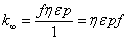
• The above formula is called four factor formula.
• The definition of each of the term is summarized.
• η is the number of second generation neutrons generated per neutron absorbed in the fuel.
• ε, called the fast fission factor is the amplification in the number of  fast neutrons due to fast fissions.
• p, called the resonance escape probability, is the fraction of fast neutrons that succeed in slowing down.
• Finally, f, the fraction of neutrons that absorb in fuel is called the thermal utilization.
• It may be noted that η ~ 2.5, ε > 1, p < 1, f < 1.
• Before we write the governing diffusion equation for two groups, it should be understood that we will write equation for both fast and thermal fluxes.
• The reactor equation for obtaining the fundamental Eigen values are same as before and the boundary conditions for both the fluxes are also same. Hence, the value of B obtained for different geometry continues to be the same as tabulated in the last lecture.