Expanding 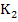 as a Taylor series about the point as a Taylor series about the point 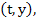 we obtain we obtain
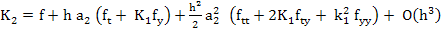
Substituting for 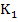 , and using (3.18), we get , and using (3.18), we get
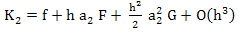 |
(3.19) |
Expanding 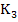 by Taylor series and after substituting for by Taylor series and after substituting for 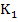 and and 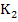 , we obtain , we obtain
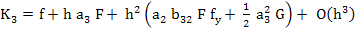 |
(3.20) |
Substituting the expansion of 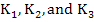 in (3.12), we have in (3.12), we have
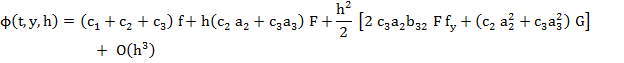 |
(3.21) |
We now have to match (3.21) with (3.16) to find the parameters. We do this in the following manner:
We first let 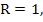 so that so that 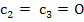 and (3.21) reduces to and (3.21) reduces to
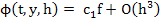 |
(3.22) |
|