To examine absolute stability of the Euler's method, we consider the test equation 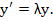 For this, we get For this, we get
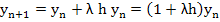 |
(2.20) |
The true solution of 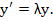 is is
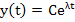 , so that by Taylor's series , so that by Taylor's series
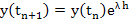 |
(2.21) |
Let 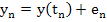 , we have from (2.20) , we have from (2.20)
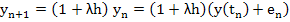
and therefore from (2.20) & (2.21), we have
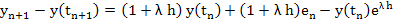
Or
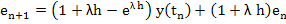 |
(2.22) |
The first expression on the RHS of (2.22) gives the local truncation error and the second expression is the inherited error. |