| |
Problems
-
Show that Euler's method fails to approximate the solution 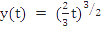 of the initial value problem of the initial value problem
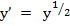 , , , , 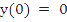 . Explain. . Explain.
-
Determine analytically the Euler approximation to the initial value problem
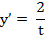 , , 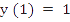 . .
Find also the exact solution of the problem and determine the magnified error function.
- How large is the discretization error of the approximation to the solution of the initial value problem
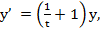 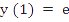
obtained by Euler's method?
-
What step size would you use with Euler's method to integrate 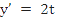 from from 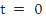 to to 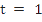 in order to achieve errors (ignoring round off errors) of not more than the following: in order to achieve errors (ignoring round off errors) of not more than the following:
• 0.1
• 0.01
• 0.001
-
Consider solving the following initial value problem by Euler's method
• 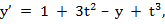 
• 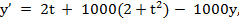 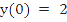
What step size would one use to achieve an error (ignore round off errors) less than
0.01?
-
Determine error bounds (a priori, a posteriori, and an error estimate) when solving the
following initial value problems over 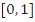 by Euler's method by Euler's method
• 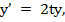 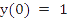
• 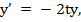 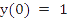
• 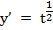 , , 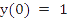
-
Determine the magnified error function for the numerical solution of the initial value
problem
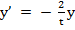 , , 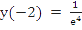
by the Euler's method.
|
|
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
|
|
|