By Taylor's formula, the expression in the brackets can be written as
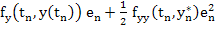
where 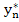 is a value between is a value between 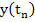 and and 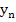 . .
We now divide (2.11) by h and introduce the quantities
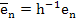 , and thus (2.11) can now be written in the form , and thus (2.11) can now be written in the form
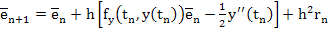 |
(2.12) |
where 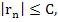 and and 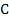 is a constant is a constant
Define the function
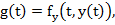 we can look at (2.12) as the result of applying Euler's method to the solution of a new differential equation for a function we can look at (2.12) as the result of applying Euler's method to the solution of a new differential equation for a function 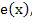
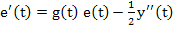 |
(2.13) |
making at each step an additional error not exceeding 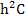 . The initial value . The initial value 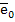 is zero, because is zero, because 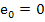 . .
|