| |
A posteriori bound
The error bound (2.8) for the solution demonstrates that the error behaves like 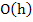 if if 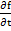 exists, is continuous, and is bounded. Generally, the function exists, is continuous, and is bounded. Generally, the function 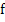 will be differentiable, and the bounds will be differentiable, and the bounds 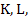 and and 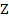 can be calculated. However, the error bound so obtained many not be very good because the largest value of can be calculated. However, the error bound so obtained many not be very good because the largest value of 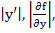 and and 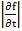 will have to be chosen. If we have some knowledge of the solution, and assume that its second derivative is continuous and bounded by a known quantity, say will have to be chosen. If we have some knowledge of the solution, and assume that its second derivative is continuous and bounded by a known quantity, say 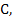 we can get a better bound. we can get a better bound.
We first express 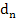 by using a Taylor's series expansion at by using a Taylor's series expansion at 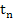 with remainder term to get with remainder term to get
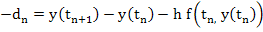
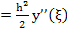 for for 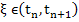
Therefore,
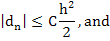
This is an A posteriori bound because it depends on knowledge of the second derivative of the solution.
|