The last term can be treated by the Mean value theorem to get a bound
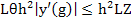
where 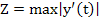 , which exists because of the continuity of , which exists because of the continuity of 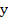 and and 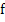 in a closed region. The treatment of the first term in (2.7) depends on our hypothesis. If we are prepared to assume that in a closed region. The treatment of the first term in (2.7) depends on our hypothesis. If we are prepared to assume that 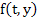 also satisfies a Lipschitz condition in t (as will happen in practice), we can bound the first term in (2.7) by also satisfies a Lipschitz condition in t (as will happen in practice), we can bound the first term in (2.7) by 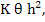 where where 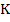 is the Lipschitz constant for is the Lipschitz constant for  as a function of as a function of 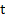 . Consequently, . Consequently,
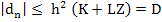
and so from (2.6), we get
Thus the numerical solution converges as 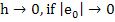 . .
|