Theorem: If 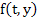 satisfies a Lipschitz condition in satisfies a Lipschitz condition in 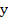 and is continuous in t for and is continuous in t for 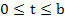 and a ll and a ll 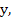 if the sequence if the sequence 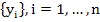 is defined by (2.1) and if is defined by (2.1) and if 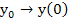 , then , then 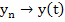 as as 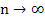 uniformly in uniformly in 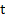 , where , where 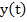 is the solution of the IVP. is the solution of the IVP.
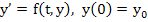 . .
Remark: We will call 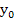 the starting value to distinguish it from the initial value the starting value to distinguish it from the initial value 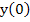 . In practice, we can only expect the starting value used in numerical computations to approach the initial value as the mesh size . In practice, we can only expect the starting value used in numerical computations to approach the initial value as the mesh size 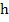 decreases and as we use more precision in our computation. In this theorem, we are assuming that (2.1) is solved without round-off errors. decreases and as we use more precision in our computation. In this theorem, we are assuming that (2.1) is solved without round-off errors.
The proof of the above theorem is given below. It consists of deriving a bound for the error
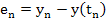
and showing that this bound can be made arbitrarily small. If a bound for the error depends only on the knowledge of the problem but not on its solution 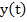 , it is called an a priori bound. If, on the other hand, a knowledge of the properties of the solution is required, its error bound is called an a posteriori bound. , it is called an a priori bound. If, on the other hand, a knowledge of the properties of the solution is required, its error bound is called an a posteriori bound.
|