| |
In order to solve (10.28), we first determine the vector Z such that
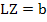 |
(10.31) |
and then y such that
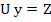 |
(10.32) |
Since 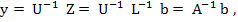 the vector y thus determined satisfies (10.28). the vector y thus determined satisfies (10.28).
In order to carry out this method, we note that (10.30) is equivalent to the relations
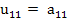 |
(10.33) |
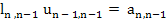 |
(10.34) |
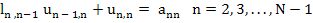 |
(10.35) |
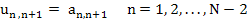 |
(10.36) |
Relation (10.36) immediately yields 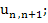 relations (10.34) and (10.35) may be rearranged to yield relations (10.34) and (10.35) may be rearranged to yield 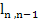 and and 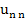 recursively, as follows: recursively, as follows:
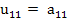 |
(10.37) |
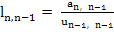 |
(10.38) |
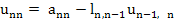 |
(10.39) |
The algorithm (10.38) and (10.39) breaks down when 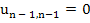 . If this is the case, then, denoting by . If this is the case, then, denoting by 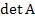 the determinant of the matrix A, we have the determinant of the matrix A, we have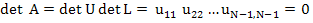 , and A is singular. , and A is singular. |
|