Finite Difference Method:
For the direct numerical solution of a boundary value problem of class 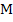 , we introduce the points , we introduce the points 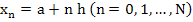 , where , where 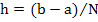 and and 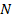 is an appropriate integer. A scheme is then designed for the determination of numbers is an appropriate integer. A scheme is then designed for the determination of numbers 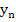 which approximate the values which approximate the values 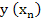 of the true solution at the point of the true solution at the point 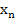 . .
The natural way to obtain such a scheme is to demand that the 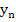 satisfy at each interior mesh point satisfy at each interior mesh point 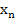 a difference equation a difference equation
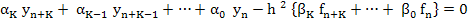 |
(10.22) |
Again the coefficients are chosen in such a way that the associated difference operator is small for a solution of 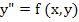 . One difficulty arises here in the difference scheme. As in any algebraic problem, we need as many equations for the determination of the unknowns as there are unknowns. Since . One difficulty arises here in the difference scheme. As in any algebraic problem, we need as many equations for the determination of the unknowns as there are unknowns. Since 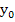 and and 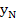 are determined by the boundary condition, the unknowns in our case are are determined by the boundary condition, the unknowns in our case are 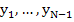 . If the step number of the difference equation . If the step number of the difference equation 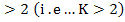 , new unknown values such as , new unknown values such as 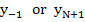 are introduced for which there is no equation. are introduced for which there is no equation.
This difficulty can be circumvented by suitably modifying the difference equations near the boundary points; it does not arise at all if 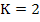 , the smallest possible value. If , the smallest possible value. If 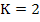 in (10.22) and if the associated–difference operator has order p, the difference equation is necessarily proportional to an equation of the form in (10.22) and if the associated–difference operator has order p, the difference equation is necessarily proportional to an equation of the form
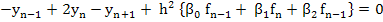 |
(10.23) |
where 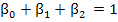 . The difference equations most frequently used for boundary value problems are. . The difference equations most frequently used for boundary value problems are.
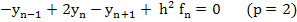 |
(10.24) |
and
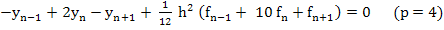 |
(10.25) |
|