Perhaps the simplest boundary value problem can be represented by the conditions
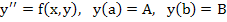 |
(10.15) |
where 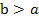 and A and B are given constants. It is theoretically always possible to reduce the solution of a boundary value problem to the solution of a sequence of initial value problems. and A and B are given constants. It is theoretically always possible to reduce the solution of a boundary value problem to the solution of a sequence of initial value problems.
Let 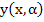 denote the solution of the initial value problem resulting from the above problem by replacing the condition for denote the solution of the initial value problem resulting from the above problem by replacing the condition for 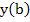 by the condition by the condition 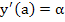 , where , where 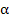 is a parameter. is a parameter.
The above boundary value problem is then equivalent to solving the (in general non linear) equation 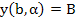 for for 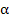 . This can be effected by one of the standard methods such as Newton's method. . This can be effected by one of the standard methods such as Newton's method.
Each evaluation of the function 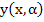 requires the solution of an initial value problem. The above ‘shooting' technique nevertheless may represent a feasible procedure. However, if the systems of differential equations are involved or if the initial value problems show signs of instability, other direct procedures may be preferable. requires the solution of an initial value problem. The above ‘shooting' technique nevertheless may represent a feasible procedure. However, if the systems of differential equations are involved or if the initial value problems show signs of instability, other direct procedures may be preferable.
Even for the simple boundary value problem considered above it may happen that there are infinitely many solutions-as in the problem
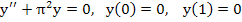 , for which , for which 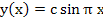 is a solution for arbitrary is a solution for arbitrary 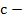 or that there is no solution, as in the problem or that there is no solution, as in the problem
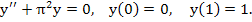
We now discuss a direct method based on implicit difference approximations for solving a class of non-linear boundary value problems of the second order. |