Euler's Method (Analytical Interpretations)
- If we approximate the derivative appearing in the differential equation at the point
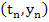 by a forward difference, we obtain by a forward difference, we obtain
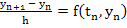
Solving for 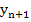 yields the formula for the Euler's method. yields the formula for the Euler's method.
- Integrating the identity
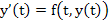
between the limits 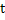 and and 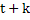 , we obtain , we obtain
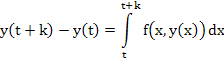
In particular, if 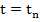 and and 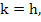 we get we get
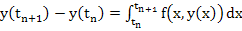
Approximating the integral by a crude rule for numerical integration (length of the interval times the value of integrand at left end point) and identifying 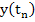 with with 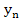 , we obtain the Euler's method. , we obtain the Euler's method.
|