Difference corrections and 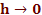 Extrapolation Extrapolation
The difference scheme given above has been shown to yield an approximation to the solution of the BVP to within an error that is 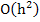 . We shall briefly examine two ways, in which, with additional calculations, the difference scheme can be made to yield . We shall briefly examine two ways, in which, with additional calculations, the difference scheme can be made to yield 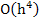 accuracy. These error reduction procedures are Richardson's deferred approach to the limit or as we prefer to call it, extrapolation to zero mesh width, and the method of difference correction. accuracy. These error reduction procedures are Richardson's deferred approach to the limit or as we prefer to call it, extrapolation to zero mesh width, and the method of difference correction.
The theoretical basis for both methods is the same, namely that some function 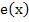 , independent of the mesh spacing , independent of the mesh spacing 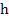 , such that the error has the form , such that the error has the form
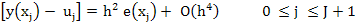 |
(10.8) |
Suppose, we compute 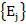 , an , an 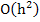 approximation to approximation to 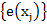 ; then clearly ; then clearly
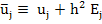
is an 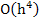 approximation to approximation to 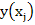 on the mesh. This is essentially the difference correction method and there may be various ways in which the on the mesh. This is essentially the difference correction method and there may be various ways in which the 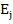 can be determined. can be determined.
For the 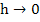 extrapolation, we solve the difference system twice, with the net spacing extrapolation, we solve the difference system twice, with the net spacing 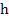 and and  . Let the respective solutions of these difference problems be denoted by . Let the respective solutions of these difference problems be denoted by 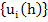 and and 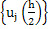 . For any point . For any point 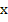 common to both meshes, say common to both meshes, say 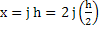 , we have from (10.8) , we have from (10.8)
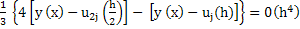 . .
Thus an 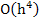 approximation to approximation to 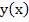 on the net with spacing on the net with spacing 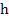 is given by is given by
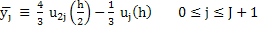 . .
A derivation of (10.8) is contained in the proof of the following: |