Linear Boundary Value Problems
Consider the single linear second-order equation
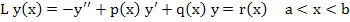 |
(10.1) |
subject to
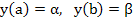 |
(10.2) |
A unique solution exists if 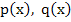 and and 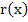 are continuous on are continuous on 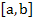 and and 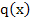 is positive there. But since these functions are continuous on a closed bounded interval, there must exist positive constants is positive there. But since these functions are continuous on a closed bounded interval, there must exist positive constants 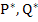 and and 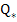 such that such that
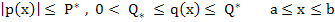
We shall now study finite difference methods for computing approximations to the solution of the BVP (10.1)-(10.2). |