| |
where 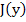 is the Jacobian matrix is the Jacobian matrix 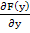 . If this method is applied to (9.3), we obtain . If this method is applied to (9.3), we obtain
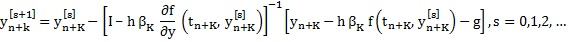 |
(9.5) |
sufficient conditions for the convergence of Newton's method for a system are rather complicated. However, when (9.5) is applied to a stiff system, Convergence is usually obtained without a restriction on 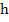 of comparable severity to that implied by (9.4), provided that we can supply a sufficiently accurate initial estimate, of comparable severity to that implied by (9.4), provided that we can supply a sufficiently accurate initial estimate, 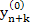 : a separate predictor can be used for this last purpose. Note, however, that (9.5) calls for the re-evaluation of the Jacobian : a separate predictor can be used for this last purpose. Note, however, that (9.5) calls for the re-evaluation of the Jacobian 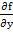 and the consequent re-inversion of the matrix and the consequent re-inversion of the matrix 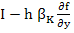 at each step of the iteration . This can be very expensive in terms of computing time, and a commonly used device is to hold the value of at each step of the iteration . This can be very expensive in terms of computing time, and a commonly used device is to hold the value of 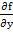 in (9.5) constant for a number of consecutive iteration steps. If the iteration converges when so modified, then it will converge to the theoretical solution of (9.3); if after a few step (typically three) it appears not to be converging, then the Jacobian is re-evaluated and the corresponding matrix re-inverted. For problems for which in (9.5) constant for a number of consecutive iteration steps. If the iteration converges when so modified, then it will converge to the theoretical solution of (9.3); if after a few step (typically three) it appears not to be converging, then the Jacobian is re-evaluated and the corresponding matrix re-inverted. For problems for which 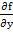 varies very slowly, it may even prove possible to hold the same value for varies very slowly, it may even prove possible to hold the same value for 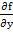 for a number of consecutive integration steps. for a number of consecutive integration steps. |