For many classes of methods (certainly for the class of linear multistep methods). A-stability, and even A(0)-stability, imply implicitness. Thus, for a linear multistep method for example, we must solve, at each integration step, a set of simultaneous non-linear equations of the form
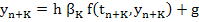 |
(9.3) |
where 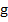 is a known vector. is a known vector.
Predictor-Corrector Techniques
Predictor-Corrector techniques prove to be inadequate when the system is stiff. If we attempt to use a 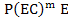 or or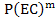 mode with fixed mode with fixed 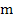 , then. The absolute stability region of the method is no longer that of the corrector alone-in general, the , then. The absolute stability region of the method is no longer that of the corrector alone-in general, the 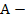 or or 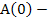 stability is lost. Nor is the mode of correcting to convergence feasible since is order that the iteration should converge we would require that stability is lost. Nor is the mode of correcting to convergence feasible since is order that the iteration should converge we would require that
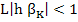 |
(9.4) |
where 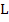 is the Lipschitz constant of is the Lipschitz constant of 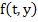 with respect to with respect to 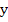 . We know that when the system is stiff, this Lipschitz constant is very large and consequently (9.4) imposes a severe restriction on step length; in practice it is of the same order of severity as that imposed by stability requirements when a method with a finite region of absolute stability is employed. . We know that when the system is stiff, this Lipschitz constant is very large and consequently (9.4) imposes a severe restriction on step length; in practice it is of the same order of severity as that imposed by stability requirements when a method with a finite region of absolute stability is employed. |