| |
The first order system 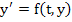 , where , where 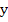 and and 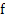 are m-dimensional vectors, is said to be linear if are m-dimensional vectors, is said to be linear if 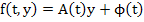 , where , where 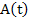 is an is an 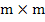 matrix and matrix and 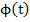 an m-dimensional vector; if in addition, an m-dimensional vector; if in addition, 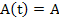 , a constant matrix, the system is said to be linear with constant coefficients. We require the general solution of such a system , a constant matrix, the system is said to be linear with constant coefficients. We require the general solution of such a system
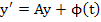 |
(9.1) |
Let 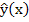 be the general solution of the corresponding homogeneous system be the general solution of the corresponding homogeneous system
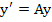 |
(9.2) |
If 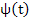 is any particular solution of (9.1), then is any particular solution of (9.1), then 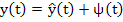 is the general solution of (9.1). is the general solution of (9.1).
A set of m linearly independent solutions 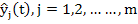 of (9.2), is said to form a fundamental system of (9.2), and the most general solution of (9.2) may be written as a linear combination of the members of the fundamental system. It is easily seen that of (9.2), is said to form a fundamental system of (9.2), and the most general solution of (9.2) may be written as a linear combination of the members of the fundamental system. It is easily seen that 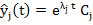 , where , where 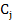 is an m-dimensional vector, is a solution of (9.2) if is an m-dimensional vector, is a solution of (9.2) if 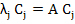 , that is, if , that is, if 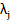 is an eigen value of A and is an eigen value of A and 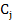 is the corresponding eigen vector. We consider only the case where A possesses m distinct possibly complex, eigen values is the corresponding eigen vector. We consider only the case where A possesses m distinct possibly complex, eigen values 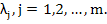 The corresponding eigen vectors The corresponding eigen vectors 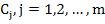 are then linearly, independent, and it follows that the solutions are then linearly, independent, and it follows that the solutions 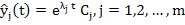 form a fundamental system of (9.2). The most general solution of (9.1) is then form a fundamental system of (9.2). The most general solution of (9.1) is then
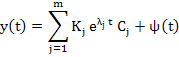
|