| |
4. Boundary Locus method: It requires neither the computation of roots of the polynomial nor the solving of simultaneous inequalities. The roots 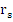 of the stability polynomial are, in general, complex numbers; for the moment let us regard of the stability polynomial are, in general, complex numbers; for the moment let us regard 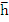 as complex. Then instead of defining an interval of absolute stability to be an interval of the real as complex. Then instead of defining an interval of absolute stability to be an interval of the real 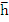 line such that the roots of line such that the roots of 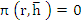 lie within the unit circle whenever lie within the unit circle whenever 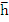 lies in the interior of the interval, we define a region of absolute stability to be a region of the complex lies in the interior of the interval, we define a region of absolute stability to be a region of the complex 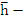 plane such that the roots of plane such that the roots of 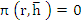 lie within the unit circle whenever lie within the unit circle whenever 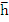 lies in the interior of the region. Let us call the region R and its boundary lies in the interior of the region. Let us call the region R and its boundary 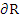 . Since the roots of the roots of . Since the roots of the roots of 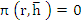 are continuous functions of are continuous functions of 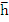 , , 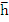 will lie on will lie on 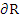 when all of the roots of when all of the roots of 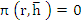 lie on the boundary of the unit circle, i.e., when lie on the boundary of the unit circle, i.e., when 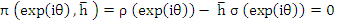 . It follows that the of . It follows that the of 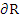 is given by is given by 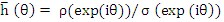 . For real . For real 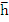 , the end points of the interval of absolute stability will be given by the points at which , the end points of the interval of absolute stability will be given by the points at which 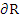 cuts the real axis. cuts the real axis.
Example: Let us illustrate the method for 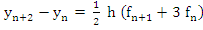 . .
For this method, 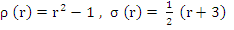
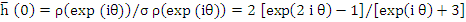
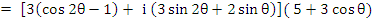
This is the locus of 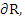 and it crosses the real axis where and it crosses the real axis where 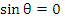 or or 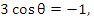 i.e. i.e.  . At . At 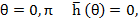 while at while at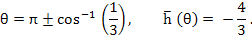 The end points of the interval of absolute stability are thus The end points of the interval of absolute stability are thus 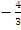 and and 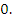 |
|