3. Routh-Hurwitz Criterion:
An alternative to Schur criterion consists of applying a transformation which maps the interior of the unit circle into the left hand half plane, and then appealing to the well-known Routh-Hurwitz criterion, which gives necessary and sufficient condition for the roots of a polynomial to have negative real parts. The appropriate transformation is 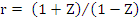 ; this maps the circle ; this maps the circle 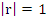 into the imaginary axis into the imaginary axis 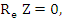 the interior of the circle into the half plane the interior of the circle into the half plane 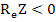 , and the point , and the point 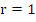 into into 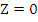 . Under this transformation, the stability polynomial becomes . Under this transformation, the stability polynomial becomes
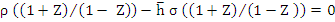 . .
On multiplying through by 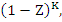 this becomes a polynomial equation of degree this becomes a polynomial equation of degree 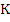 , which we write , which we write
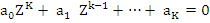 |
(8.37) |
where, we assume without loss of generality that 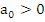 . The necessary and sufficient condition for the roots of (8.37) to lie in the half plane . The necessary and sufficient condition for the roots of (8.37) to lie in the half plane 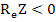 , that is, for the roots of , that is, for the roots of 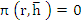 to lie within the circle to lie within the circle 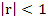 , is that all the leading principal minors of , is that all the leading principal minors of 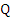 be positive, where be positive, where 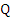 is the is the  matrix defined by matrix defined by
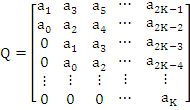
and where 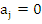 if if 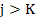 . It can be shown that this condition implies . It can be shown that this condition implies 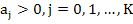 . Thus the positivity of the coefficients in (8.37) is a necessary but not sufficient condition for absolute stability. For . Thus the positivity of the coefficients in (8.37) is a necessary but not sufficient condition for absolute stability. For 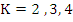 the necessary and sufficient condition for absolute stability given by this criterion are as follows, the necessary and sufficient condition for absolute stability given by this criterion are as follows,
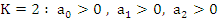 . .
K = 3 : 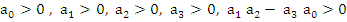 |