Using the device described above to find, for this example, the interval of relative stability, given by the requirement 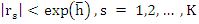 , we consider the polynomial , we consider the polynomial
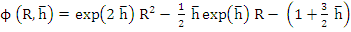 . Then . Then
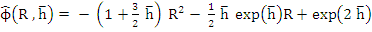
and we obtain the first condition
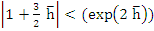
After a little manipulation, we find that the first degree polynomial 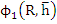 is Schur if and only if is Schur if and only if
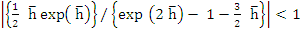 . .
A full solution of this pair of simultaneous inequalities for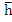 involves considerable computation but on expanding the exponentials in powers of involves considerable computation but on expanding the exponentials in powers of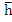 , it becomes clear that both inequalities are satisfied for all positive , it becomes clear that both inequalities are satisfied for all positive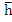 and that the second is not satisfied for small negative and that the second is not satisfied for small negative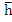 . We conclude that . We conclude that 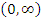 is an interval of relative stability. is an interval of relative stability. |