Let us return to our stability analysis and let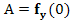. Then the stability of the non-linear autonomous system (1.12) is related to that of the linear system

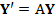
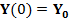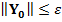
The solution of this system is

(1.15)

where the matrix exponential is defined by the series

(1.16)

Often, the matrix A can be diagonalized as

where are the eigen values of A and the columns of T are the corresponding eigen vectors. In this case, we may easily verify that the solution of (1.14) is

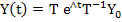
Thus, (1.14) is stable if all of the given values have non-positive real parts, and asymptotically stable if all of the eigen values have negative real parts, and unstable otherwise.