Theorem:
A stable and consistent linear multistep method is convergent.
Proof: Let the function 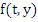 satisfy the conditions of the existence and uniqueness, and let satisfy the conditions of the existence and uniqueness, and let 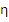 be an arbitrary constant. We shall denote by be an arbitrary constant. We shall denote by 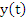 the solution of the initial value problem the solution of the initial value problem 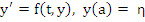 . Let . Let 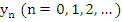 be the solution of the difference equation (8.1), defined by the starting values be the solution of the difference equation (8.1), defined by the starting values
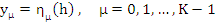 . We set . We set
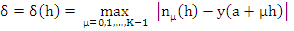
and assume that
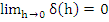 |
(8.21) |
We then have to show that for any 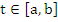
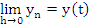
We begin by estimating the quantity 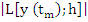 , where , where 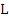 denotes the difference operator defined earlier. denotes the difference operator defined earlier.
The function 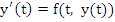 is continuous in the closed interval is continuous in the closed interval 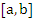 . We define for . We define for 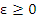 the quantity the quantity
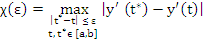
For 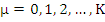 , we can write , we can write
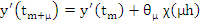
where 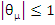 . Furthermore, since . Furthermore, since
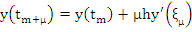
where 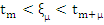 , we have , we have
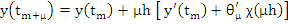
|