Illustrative Examples
Example 1: If 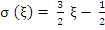 and and 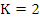 , we get , we get
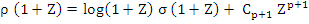
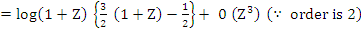
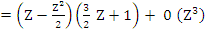
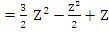
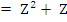
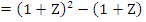
Hence 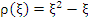 , which gives the second order Adams-Bashforth method , which gives the second order Adams-Bashforth method
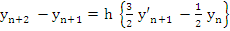
or 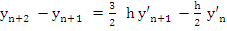
If, on the other hand, 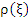 is given, there exists a is given, there exists a 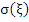 of degree K such that the method is of order of degree K such that the method is of order 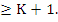 We find this by dividing (8.8) by log We find this by dividing (8.8) by log 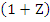 to get to get 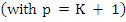
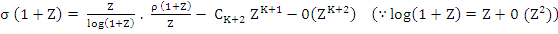 . .
Since 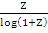 is analytic at is analytic at 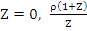 must be analytic at must be analytic at 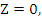 if if 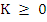 , that is, , that is,
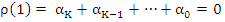
Example 2: If 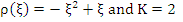 we get we get
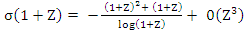
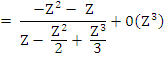
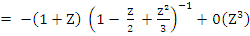
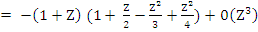
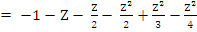
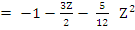
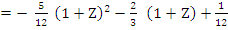
Hence, 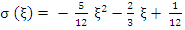 , which gives the third order Adams-Moulton method: , which gives the third order Adams-Moulton method:
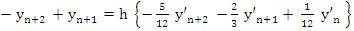
|