we obtain
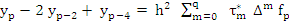 |
(7.52) |
where
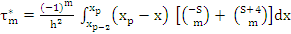
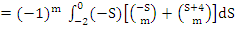 |
(7.53) |
The generating function is given as:
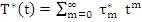
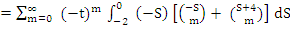
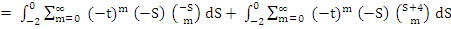
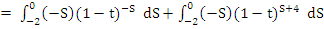
on integration, we find
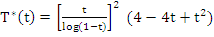 |
(7.54) |
The recurrence relation is obtained as
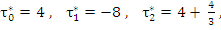
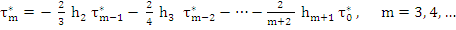
By comparing (7.50) and (7.54), we also find that

The numerical values of 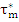 are readily found as follows: are readily found as follows:
For 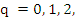 (7.52) has an irregular appearance, and its use for practical purposes is not recommended. For (7.52) has an irregular appearance, and its use for practical purposes is not recommended. For 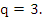 , the formula reads , the formula reads
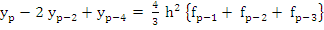 |
(7.55) |
which is equivalent to (7.51). For 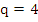 and, since and, since 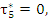 also for also for 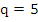 , (7.52) reduces to , (7.52) reduces to
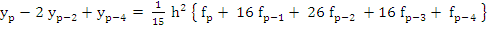 |
(7.56) |
|