Using integration by parts, we get
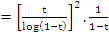 |
(7.40) |
From
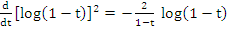
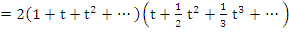
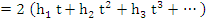
where 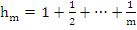 denotes the denotes the 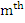 partial sum of the harmonic series. partial sum of the harmonic series.
Thus it follows
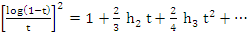 |
(7.41) |
Multiplying both sides of (7.41) by (7.40), we thus find
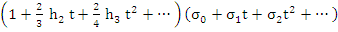
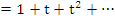
There follows the recurrence relation
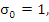
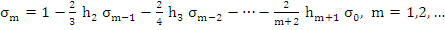
The numerical values of  for a few values of m are given in the following table: for a few values of m are given in the following table:
Formula (7.38) is used in much the same manner as the Adams-Bashforth formula. Once the values  are known, are known, 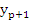 can be calculated explicitly, without iteration. can be calculated explicitly, without iteration.
For 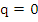 and and 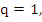 stormer's formula reduces to the simple rule stormer's formula reduces to the simple rule
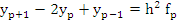 |
(7.42) |
|