| |
Since 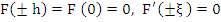 for some for some 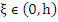 . But . But
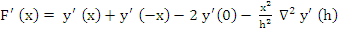
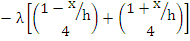
vanishes also for 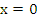 and and 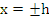 . Thus, in view of the fact that . Thus, in view of the fact that 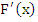 has five distinct zeros in the closed interval has five distinct zeros in the closed interval 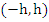 , the fifth derivative , the fifth derivative 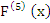 has at least one zero in has at least one zero in 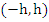 , the fifth derivative , the fifth derivative 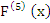 has at least one zero in has at least one zero in 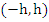 . We easily find . We easily find
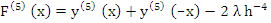
and thus have, for some 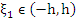
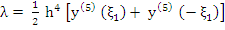
But, by the continuity of 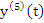 it follows as before that it follows as before that
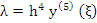
for some  between between 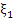 and and  . Inserting this value in (7.31), (7.29) follows: . Inserting this value in (7.31), (7.29) follows: |