| |
iv) The Generalized Milne-Simpson Method:
Here we have
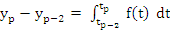
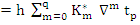 |
(7.18) |
where
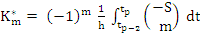
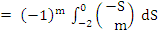 |
(7.19) |
Formula (7.18) resembles the Adams-Moulton formula in being implicit. However, the integration is now over two steps, which may cause weak stability. On the other hand, the method is, for comparable 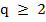 , more accurate than any of the methods previously considered. This is true in particular in the case , more accurate than any of the methods previously considered. This is true in particular in the case 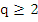 , which is known as the Milne method. The reason why it is more accurate will be understood by studying the coefficients , which is known as the Milne method. The reason why it is more accurate will be understood by studying the coefficients 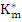 . Their generating function is given by . Their generating function is given by |