The numerical values given in the above table suggest that (7.18) be better written and used in the form
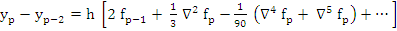 |
(7.21) |
The Milne formula resulting from 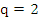 or or 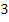 may be written out in terms of ordinates as follows may be written out in terms of ordinates as follows
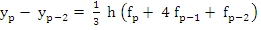 |
(7.22) |
Equations (7.18), (7.21) and (7.22) represent implicit equations for 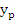 and are usually solved by iteration, starting with a predicted first approximation and are usually solved by iteration, starting with a predicted first approximation 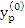 . Any explicit formula can be used in principle to calculate . Any explicit formula can be used in principle to calculate 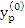 . In the interest of economizing the number of corrections, one will choose, if possible, a predictor formula whose accuracy is comparable to that of the corrector formula. Milne suggests the formula . In the interest of economizing the number of corrections, one will choose, if possible, a predictor formula whose accuracy is comparable to that of the corrector formula. Milne suggests the formula
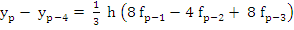 |
(7.23) |
(resulting from integrating the quadratic polynomial interpolating 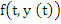 at at 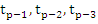 between between 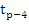 and and 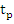 ) as a predictor formula. Now the iteration procedure may be arranged in the same manner as explained in Adams-Moulton method. ) as a predictor formula. Now the iteration procedure may be arranged in the same manner as explained in Adams-Moulton method. |