Problems

1. Prove that the alternative solutions given in (6.12) both lead to the same method given by (6.13).

2. Show that when 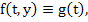the implicit method (6.13) reduces to a quadrature formula which is equivalent to the two- point Gauss-Legendre quadrature formula .
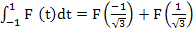3. In addition to (6.13), Hammer and Hollingsworth proposed the method

   

   

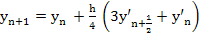
   where, ..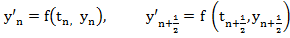

   Write this method in the form (6.1)-(6.3) and use (6.8)-(6.11) to show that it is of third order.

4. Prove that the semi–explicit method (6.14) has order four and find its interval of absolute stability.
5. Find the order of the Implicit Runge-Kutta method

   

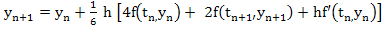
   and determine its interval of absolute stability.

6. Find the order of the method

   

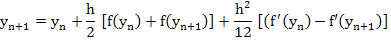
   where 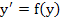.