Now from (6.2) with 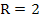 , we have , we have
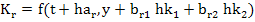 , , 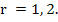
Expanding 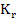 by Taylor series about by Taylor series about 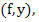 we get we get
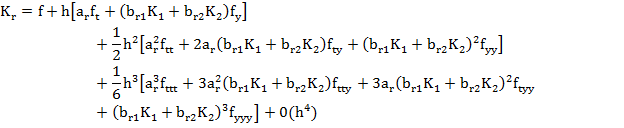 |
(6.5) |
Since these two equations are implicit, we can no longer proceed by successive substitution as done in the case of explicit Runge-Kutta methods earlier. Let us assume instead, that the solutions for 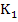 and and 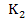 may be expressed in the form may be expressed in the form
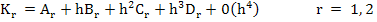 |
(6.6) |
Substituting for 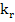 by (6.6) in (6.5) we get by (6.6) in (6.5) we get
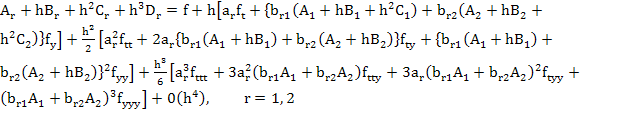
|