Problems

1. Find the local truncation error of the mid-point method given by (3.5).

2. Find the local truncation error of the trapezoidal rule given by (3.9).
3. Find condition on the value of 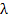such that if the mid-point method is used to solve

   

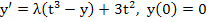
   over 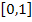, then the error will be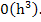

4. Determine the order of the method given by

   

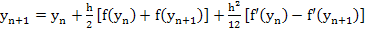
   where .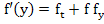

5. Prove that the differential equation y' 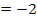at is solved exactly by the mid-point method (3.5).

6. Show that the method given by

   

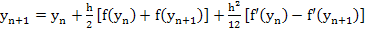
   is of order 3.

7. Let 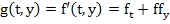. Prove that the single-step method defined by the increment function

   

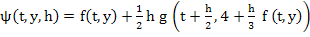
   has order 3.

8. Determine the principal error function of the trapezoidal method given by (3.9).

9. Show that for the problem

   

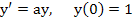
   the midpoint method is identical with the Taylor series method of order 2, and the classical Runge-Kutta method is identical with the Taylor series method of order 4.