|
which is called a canonical representation of (1.2). In such a form, the highest order derivative is expended in terms of lower order derivatives and the independent variable. It is known that the general solution of the 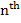 order ODE contains order ODE contains 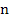 independent arbitrary constants. In order to determine a particular solution or to describe a specific physical situation, supplementary conditions to determine the arbitrary constants in the general solution are prescribed. If these supplementary conditions are prescribed at one point, then these conditions are called initial conditions and if the conditions are prescribed at more than one point, then these are called boundary conditions. independent arbitrary constants. In order to determine a particular solution or to describe a specific physical situation, supplementary conditions to determine the arbitrary constants in the general solution are prescribed. If these supplementary conditions are prescribed at one point, then these conditions are called initial conditions and if the conditions are prescribed at more than one point, then these are called boundary conditions.
The differential equation together with the initial conditions is called an Initial Value Problem (IVP) and the differential equation together with the boundary conditions is called a Boundary Value Problem (BVP).
|