| Lectures 31 - 33 |
| In this chapter, we introduce the notion of characteristic function of a
random variable and study its properties. Characteristic function serves
as an important tool for analyzing random phenomenon. |
Definition 7.1 (Characteristic functions)
The characteristic function of a random variable 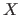 is defined as is defined as |
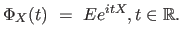 |
(where
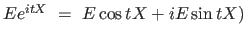 |
Example 7.0.43 Let
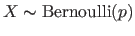 . Then . Then |
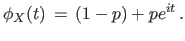 |
Example 7.0.44 Let
 . Then . Then |
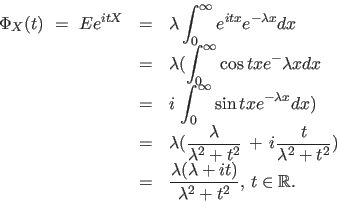 |