| |
| Lectures 4 - 7 |
In many situations, one is interested in only some aspects of the random experiment. For example,
consider the experiment of tossing  unbiased coins and we are only interested in number of
'Heads' turned up. The probability space corresponding to the experiment of tossing unbiased coins and we are only interested in number of
'Heads' turned up. The probability space corresponding to the experiment of tossing  coins is given by coins is given by |
| |
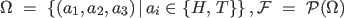 |
|
and 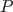 is described by is described by |
| |
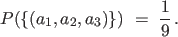 |
|
Our interest is in noting
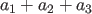 , i.e.,
in the map , i.e.,
in the map
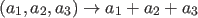 . So our interest is only on certain function
of the sample space. But all functions defined on the sample space are not useful, in the sense
that we may
not be able to assign probabilities to all basic events associated with the function. So one
need to restrict to certain class of functions of the sample space. This motivates us to define
random variables. . So our interest is only on certain function
of the sample space. But all functions defined on the sample space are not useful, in the sense
that we may
not be able to assign probabilities to all basic events associated with the function. So one
need to restrict to certain class of functions of the sample space. This motivates us to define
random variables. |
Definition 2.1 Let
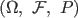 be a probability space.
A function be a probability space.
A function
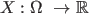 is said to be a random variable if is said to be a random variable if |
| |
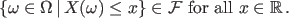 |
|
Now on, we denote
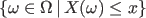 by by
 . . |
|
|
|