Chapter 1
Introduction
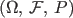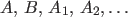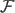Theorem 1.0.1 (Properties of probability measure)   Let $ (\Omega, \, {\mathcal F}, \, P)$ a probability space and $ A, \, B, \, A_1 , \, A_2 , \dots $are in $ {\mathcal F}$. Then
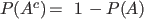(1) $ P(A^c) \ = \ 1 \ - \ PA$ .
(2) Finite sub-additivity:
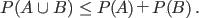  $\displaystyle P({A\cup B}) \ \leq \ { PA} \ + \ {PB} \, .$  
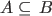(3)Monotonicity: if $ A \subseteq \, B$, then
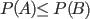  $\displaystyle PA \, \leq \, P B \, .$  
(4)Boole's inequality (Countable sub-additivity):
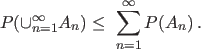  $\displaystyle P(\cup^{\infty}_{n=1} A_n) \leq \ \sum^{\infty}_{n=1} {P(A_n)} \, .$  
(5)Inclusion - exclusion formula:
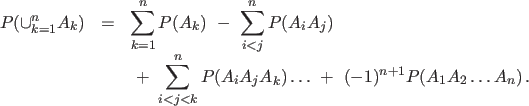  \begin{displaymath} \begin{array}{lll} P(\cup^n_{k=1}{A_k}) & = & \displaystyl... ...s \ + \ (-1)^{n+1} P(A_1A_2 \dots A_n) \, . }\\ \end{array} \end{displaymath}  
(6)Continuity property:
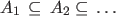(i) For $ A_1 \, \subseteq \, A_2 \subseteq \, \dots$
  $\displaystyle P(\cup^{\infty}_{n=1} A_n) \ = \ \lim_{n \to \infty} P(A_n) \, .$  
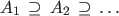(ii) For $ A_1 \, \supseteq \, A_2 \, \supseteq \, \dots $ ,
  $\displaystyle P({\cap}^{\infty}_{n=1} A_n) \ = \ \lim_{n \to \infty} P(A_n) \, .$