| Definition 1.2 ( Event ) Any subset of a sample space is said to be an
event. |
Example 1.0.4 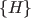 is an event corresponding to the sample space in Example 1.0.1. is an event corresponding to the sample space in Example 1.0.1. |
Definition 1.3 (mutually exclusive events) Two events 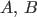 are said to be
mutually exclusive if are said to be
mutually exclusive if
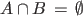 . .
If 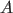 and and 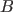 are mutually exclusive, then occurrence of are mutually exclusive, then occurrence of 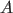 implies non occurrence of implies non occurrence of 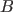 and vice versa.
Note that non occurrence of and vice versa.
Note that non occurrence of 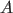 need not imply occurrence of need not imply occurrence of 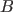 , since , since
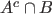 need not be need not be 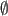 . . |
| |
Example 1.0.5 The events 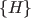 , ,  of the sample space in Example 1.0.1 are mutually exclusive. But the events of the sample space in Example 1.0.1 are mutually exclusive. But the events
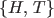 , ,  are not mutually exclusive. are not mutually exclusive. |
Now we introduce the concept of probability of events (in other words probability measure).
Intuitively probability quantifies the chance of the occurrence of an event. We say that an event
has occurred, if the outcome belongs to the event. In general it is not possible to assign probabilities
to all events from the sample space. For the experiment given in Example 1.0.3, it is
not possible to assign probabilities to all subsets of ![$ (0, \ 1]$](../../images/lec1/img17.png) . So one need to restrict to a
smaller class of subsets of the sample space. For the random experiment given in Example 1.0.3, it turns out that one can assign probability to each interval in . So one need to restrict to a
smaller class of subsets of the sample space. For the random experiment given in Example 1.0.3, it turns out that one can assign probability to each interval in ![$ (0, \ 1]$](../../images/lec1/img17.png) as its length. Therefore, one can assign probability to any finite union of intervals in as its length. Therefore, one can assign probability to any finite union of intervals in ![$ (0, \ 1]$](../../images/lec1/img17.png) , by representating the finite union of intervals as a finite disjoint union of intervals. In fact one can assign probability to any countable union interval in , by representating the finite union of intervals as a finite disjoint union of intervals. In fact one can assign probability to any countable union interval in ![$ (0, \ 1]$](../../images/lec1/img17.png) by preserving the desirable property "probability of countable disjoint union is the sum of probabilities". Also note that if one can assign probability to an event, then one can assign probability to its compliment, since occurence of the event is same as the non-occurance of its compliemt. Thus one seek to define probability on those class of events which satisfies "closed under complimentation" and "closed under countable union". This leads to the following special family of events
where one can assign probabilities. by preserving the desirable property "probability of countable disjoint union is the sum of probabilities". Also note that if one can assign probability to an event, then one can assign probability to its compliment, since occurence of the event is same as the non-occurance of its compliemt. Thus one seek to define probability on those class of events which satisfies "closed under complimentation" and "closed under countable union". This leads to the following special family of events
where one can assign probabilities. |
|
|
|