The proof of Mayer Vietoris sequence is reminiscent of the Seifert Van Kampen theorem.
While the Seifert Van Kampen theorem enables us to relate the fundamental group of a union 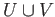 in terms of
the fundamental groups of in terms of
the fundamental groups of 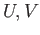 ,and ,and 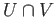 , the situation here is slightly more involved.
The precise relationship between the homologies of , the situation here is slightly more involved.
The precise relationship between the homologies of
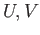 and and 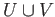 is described in terms of the long exact
sequence of theorem (34.7). is described in terms of the long exact
sequence of theorem (34.7).
As in the Seifert Van Kampen theorem we obtain from a push-out diagram of topological spaces a push out diagram of
chain complexes which turns into a short exact sequence of complexes. The corresponding long-exact sequence gives, after
an application of the excision theorem of the last lecture,
the Mayer Vietoris sequence. It is one of the most efficient tools available for the computation of homology groups.
We restate here the theorem for convenience.
Theorem 35.1:
Suppose  and and  are subsets of a topological space such that
Int Int are subsets of a topological space such that
Int Int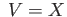 . Then there is a long exact sequence . Then there is a long exact sequence
|