Module 4 : Theory of covering spaces
Lecture 19 : Deck transformations
 

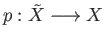Given a covering projection $ p: \tilde{X} \longrightarrow X$, the deck transformations are, roughly speaking, the symmetries of the covering space. Thus it should not come as a surprise that they play a crucial part in the theory of covering spaces. In this lecture all spaces are assumed to be connected and locally path connected.

Definition 19.1 (Deck transformations):

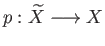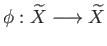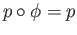Let $ p : \widetilde X \longrightarrow X$ be a covering projection. A deck transformation is a homeomorphism $ \phi : \widetilde X \longrightarrow \widetilde X$ such that $ p \circ \phi = p$, that is to say $ \phi$ is a lift of $ p$.

Examples 19.1:

(i) For the covering space ex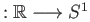$ : \mathbb{R} \longrightarrow S^1$ given by ex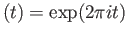$ (t) = \exp(2\pi it)$ the deck transformations are the maps
$\displaystyle T_n :\mathbb{R} \longrightarrow \mathbb{R}, \quad T_n(x) = x + n,\quad n\in\mathbb{Z} $
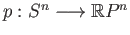(ii) For the two sheeted covering $ p : S^n \longrightarrow \mathbb{R}P^n$ the deck transformations are the identity map and the antipodal map.

The following theorem summarizes the most basic properties of the group of deck transformations.