Let 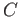 be a closed subset of
be a closed subset of  . Since
. Since 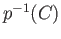 is closed in
is closed in 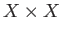 we note that
we note that
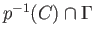 is closed in
is closed in 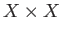 and hence is compact. Thus
and hence is compact. Thus
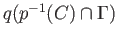 is compact and so is closed in
is compact and so is closed in  . Now,
. Now,
showing that 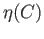 is closed. This proves (a) and in particular we note that singleton sets in
is closed. This proves (a) and in particular we note that singleton sets in 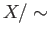 are closed since they are images of singletons. Turning to the proof of (b), for an arbitrary
pair of distinct elements
are closed since they are images of singletons. Turning to the proof of (b), for an arbitrary
pair of distinct elements
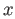 and
and
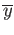 in
in 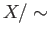 , the sets
, the sets
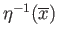 and
and
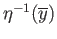 are a
pair of disjoint closed sets in
are a
pair of disjoint closed sets in  . Since
. Since  is normal there exist disjoint open sets
is normal there exist disjoint open sets  and
and  in
in  such that
such that
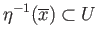
and
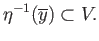
The sets 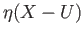 and
and 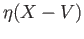 are closed in
are closed in 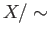 by (a). We leave it to the reader to verify
that the complements
by (a). We leave it to the reader to verify
that the complements
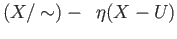
and
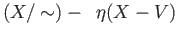
are disjoint sets. Now
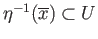 implies
implies
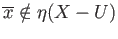 whereby
whereby
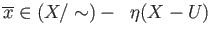 . Likewise
. Likewise
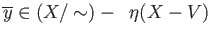 and the proof is
complete.
nisha
2012-03-20
and the proof is
complete.
nisha
2012-03-20