The quotient of a Hausdorff space need not be Hausdorff. Since quotient spaces occur in abundance we need
easily verifiable sufficient conditions for a quotient space to be Hausdorff. We provide here one such condition
which suffices for most applications [16].
Let  be a space on which an equivalence relation
be a space on which an equivalence relation 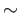 has been defined.
Note that a relation on
has been defined.
Note that a relation on  is a subset
is a subset 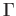 of the cartesian product
of the cartesian product 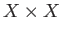 on which we have the product
topology. Thus,
on which we have the product
topology. Thus,
nisha
2012-03-20